Contact:
Brillouin light scattering is generally referred to as inelastic scattering of an incident optical wave field by thermally excited elastic waves in a sample. Light scattering from thermally excited acoustic waves was theoretical predicted by L. Brillouin1. Later Gross2 experimentally confirmed that prediction in liquids and in crystals. Brillouin spectroscopy did not show obvious progress until the 1960s, due to a lack of the proper light sources. In 1960, the invention of the laser solved the light source problem; since then Brillouin light scattering techniques have earned reasonable attentions and has been widely used.
The Fabry-Perot interferometer has been the instrument of choice in most Brillouin experiments. However, conventional Fabry-Perot interferometers do not achieve the contrast needed to resolve the weak Brillouin peaks. Sandercock first suggested that if two synchronized Fabry-Perot interferometers were coupled, it would significantly improve the contrast and achieve the resolution that necessary to resolve the weak Brillouin doublets3 (see Fig. 2).
In the case of a transparent solid (crystals or glasses), the incident laser light will induce dynamic fluctuations in the strain field to bring about fluctuations in the dielectric constant, and these in turn translate into fluctuations in the refractive index due to the elasto-optic scattering mechanism. These fluctuating optical inhomogeneities result in inelastic scattering of the light as it passes through the solid.
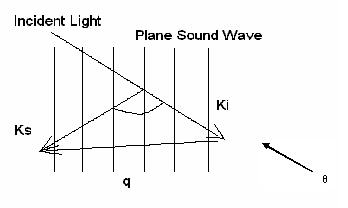
Figure 1: The principle of light scattering from sound wave in materials.
The phonons present inside a solid move in thermal equilibrium with very small amplitudes creating fluctuations in the dielectric constant, which is viewed as a moving diffraction grating by an incident light wave. Therefore Brillouin scattering can be explained by the concepts of Bragg reflection and Doppler shift.

Figure 2: Sandercock type Tandem Fabry-Perot interferometer.

Figure 3: Brillouin light scattering stages.
The moving grating scatters the incident light with a Doppler effect, giving scattered photons with shifted frequencies Δv. Brillouin spectrum gives frequency shift (Δv) of the thermal phonon, and its wavelength (d space) can be determined from the experiment geometry. For instance (Fig.1), if the ni as the refractive index in direction of incident light, the ns as the refractive index in scattering direction, and the υ as the velocity of acoustic phonons, then the Brillouin shift Δv is given as follows:
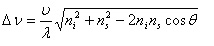 (1)
(1)
where λ is the wavelength of incident light and θ is the scattering angle.
The Micro-Brillouin apparatus are shown in Figs. 2 and 3, experimental details were reported in Ref4. This is a non-contact measurement technique that exploits light scattering to probe the elastic properties of liquids and solids (crystals). In the Geophysical Laboratory of the Carnegie Institution of Washington, the Brillouin scattering technique has been combined with diamond anvil cells and intensively used in variety research areas, including geophysics4, mineral physics4, 5, liquids6, dense gases6, phase transitions7, and ferroelectrics8, 9.
